Applied Complexity Newsletter - September 2020

Applied Complexity Newsletter
September 2020
Seasons Changing
Fall is in the air here in New Hampshire. At times it is hard to emotionally reconcile the drama going on in the world with our quiet little homestead. My hope is that the world comes to resemble more our home, and not the other way around. Even so, we continue to push forward with the assumption that society as we have come to know it is not a given.
Civil Unrest and Phase Transitions
There are signs that precede phase transitions. “Critical slowing down” for instance means that perturbations that push a system away from stable points start sending the system further away, and the system takes longer to return, and “flickering” can be observed when a stochastic system switches back and forth between states more readily and rapidly than previously.
To illustrate the idea, I ran two simulations of the simplest attractor dynamics possible, with an additional noise term whose parameters we hold constant throughout the simulation:
(1) - Simple attractor with noise
dx/dt = Lx + e(t)
When L is negative, we have an attractor — trajectories tend to flow to this point from around it, and perturbations, here represented by the noise term e(t), can push the variable x away from the attractor, but it will tend to return.
The more negative L is, the stronger the attractor. One way to look at that is the so-called potential function (figure below), which is the negative anti-derivative of the differential equation. The potential function allows us to visualize stability in terms of maxima and minima — we can imagine a ball on the function that rolls and wants to settle into the dips, and roll off of the hill tops. The figure on the right shows five potential functions for different values of L. The blue curve corresponds to L = -40, and represents the strongest attractor pictured. Trajectories will find their way quickly down the slope to the valley. The less steep curves have less attractive force. The flat purple curve represents a complete loss of stability.

In the simulation we slowly transition the L parameter to values that are less and less stable. Again, we keep the perturbations constant throughout (normally distributed with a standard deviation of one). We notices that despite the fact that the perturbations do not get any larger, the deviations from the attractive point (x=0) become larger and last longer. That is critical slowing down.

At L=0 a phase transition occurs. The point x=0 changes from a stable attractor to an unstable repeller. Here is a second simulation where that threshold is crossed.
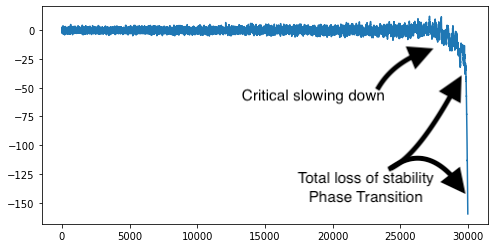
The civil unrest we are experiencing in the US is not entirely unprecedented, but it does appear that we are moving further from the stable attractor we’ve come to know as American Society, and for longer. And too many cities have flickered in and out of violent clashes and lawless rioting to feel confident that this will subside and things will return to “normal”.
I am not here to lay blame on anyone — it is clear that the situation is systemic. Systemic in the sense that the events that are trigger cascades of unrest are not the *cause* of the unrest itself. Much like how a given spark may happen to start a forest fire, but it is the state of the forest itself that makes the fire inevitable. A spark always comes, eventually.
This helps to explain why what the unrest was purportedly about, unnecessary and unjustified police violence, has been lost in the noise. These are trigger events. The forces in tension would not be resolved even if we did find solutions to overreaches in policing. Which is a damn shame. (Qualified immunity and questions of whether police have enough skin in the game in the communities they police are legitimate issues.)
Where is the next stable point after the phase transition? No one can say. But in my view it is time to start focusing locally. If your local environment isn’t habitable than anything beyond it is moot.
Self-sufficiency
A recent tweet that quoted Russ Roberts from EconTalk (@econtalker on Twitter) caught my eye the other day. It read “Self-sufficiency if the road to poverty.”
Given Russ’s professional focus, I’m certain this comment follows from the centrality of the division of labor and specialization made famous in Adam Smith’s work on economics. The basic idea is that by each agent getting very good at one thing, and splitting up tasks among agents, together the collective is much better at all the things it does then it would be if each person had to all the things themselves in a mediocre fashion.
It is clear that division of labor is essential to the proper functioning of human collectives and economies. And to refuse to divide labor would certainly be a sure way to remain impoverished. However the perspective offered by the tweet, and by the mere abstract division of labor, misses several important aspects of the ideal of self-sufficiency and its essential role in individual and collective prosperity.
Knowhow is gained only through experience. It takes time and is not immediate. When we divide labor such that knowhow of essential functions is held in specialist individuals only, any disruption to the transactional network can put individuals who lack essential knowhow in a tough spot, to put it lightly.
Moreover, knowhow yields optionality. If I acquire the skills to, say, install my own plumbing, it does not mean that I can’t hire a plumber to do my plumbing work for me when the conditions make that favorable. However if I never learned any basic plumbing and I have a burst pipe and no plumber, I’m SOL as they say.
Clearly there is a limit. One can’t learn every skill to an expert level. But one can learn many essentials to a sufficient level, such that if needed one can rely on these skills.
When we forfeit all knowhow except for a very narrow and specialized domain, we fragilize ourselves to disruptions and changes in our context and environment. What when the social phase transition does happen? Will those with ability to remain self-sufficient be the most impoverished, or the most prosperous? Life is dynamic.
Spring 2020 Intro to Complexity and Applied Complexity - enrollment opening soon
In two weeks the first session of the Intro to Complexity and Applied Complexity course kicks off. I’ve been organizing class materials and session topics — I can’t wait!
In the coming days I will be opening up enrollment for two additional Spring sessions. I plan to keep enrollment limited once again as I am already pleased with the pre-course dynamics occurring on our discord server. Small is beautiful.
Thanks for reading and don't hesitate to reach out joe.w.norman@gmail.com
All my best,
Joe
